Teorema sulla continuità delle funzioni derivabili. Home page. Analisi. Classe quinta. TEOREMA SULLA CONTINUITA' DELLE FUNZIONI DERIVABILI . Enunciato: Se la funzione y = f (x) è derivabile nel suo punto di ascissa x. 0 allora è ivi continua. Cioè: . Hp: f ( x 0 ) Ts: limh → 0 f (x 0 + h ) = f ( x 0 ) Dimostrazione: .. Brevemente: La derivata della somma di due funzioni derivabili esiste ed è uguale alla somma delle derivate": y = f ( x ) + g ( x ) → y ' = f '( x ) + g '( x ) Altri modi di schematizzare il teorema possono essere: ( f + g )' = f ' + g ' , D [ f ( x ) + g ( x ) ] = Df ( x ) + Dg ( x ) Dimostrazione.

Matematica Modulo 2 Una funzione derivabile è continua Se una funzione è derivabile si può

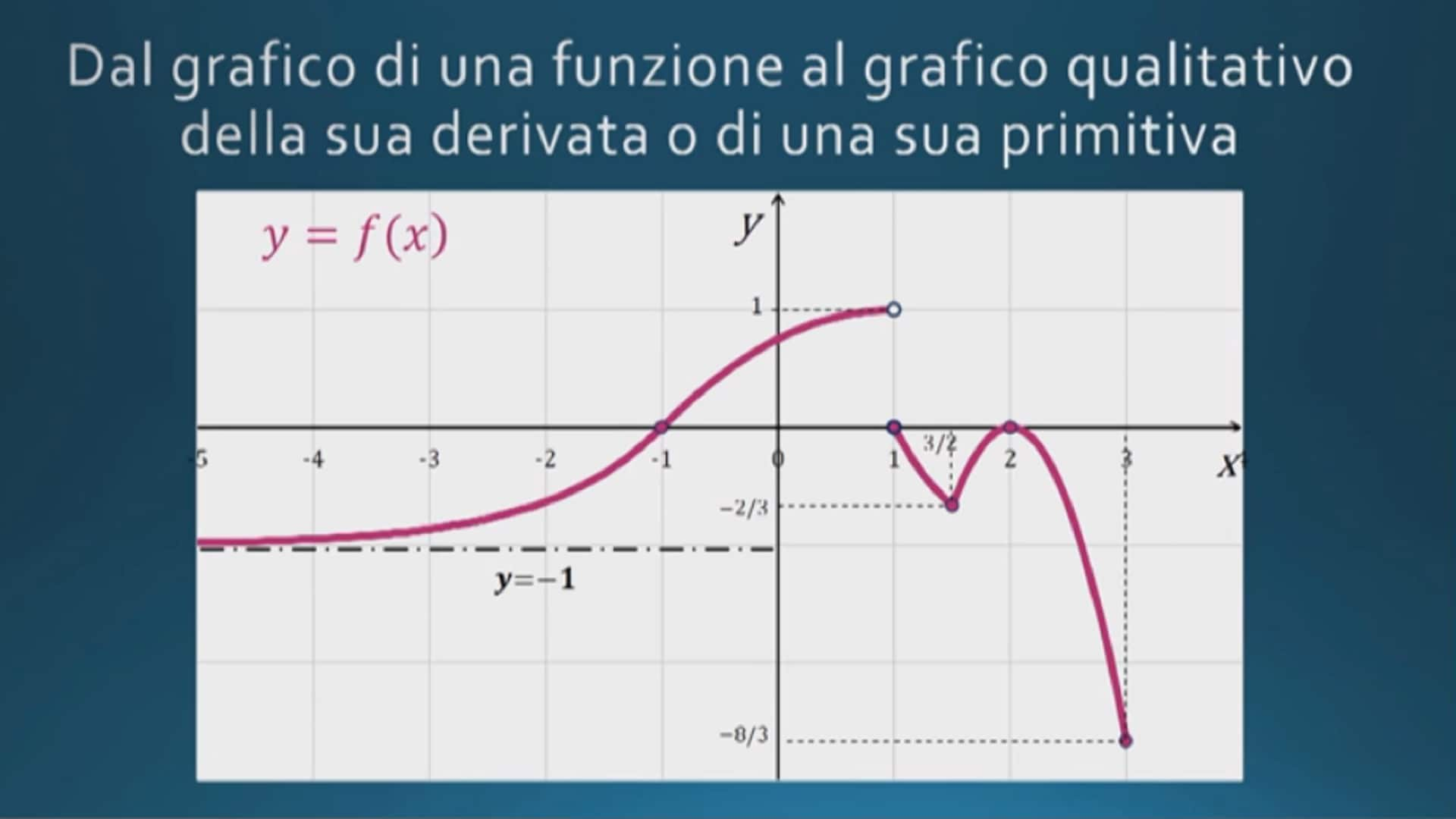
Dal grafico di una funzione a quello della sua derivata o di una sua primitiva Matematica

Funzioni continue

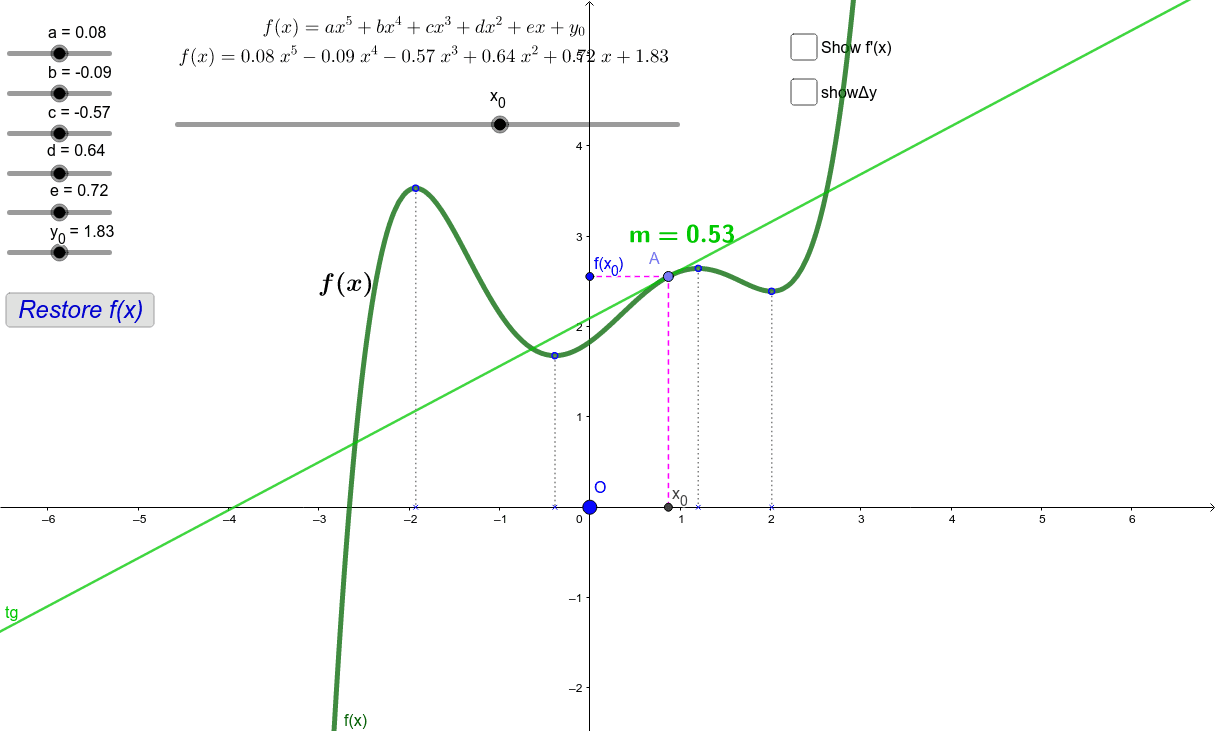
Il grafico di una funzione e della sua derivata GeoGebra

I teoremi delle funzioni derivabili ppt scaricare

Esercizi svolti continuità e derivabilità delle funzioni con Taylor matematica & oltre

La Continuità di una Funzione in un Suo Punto & Le Funzioni Continue YouTube

Funzioni e derivate Il concetto di derivata Il

PPT LA DERIVATA DI UNA FUNZIONE PowerPoint Presentation, free download ID2434290

Funzione derivabile, esercizio svolto YouTube

Studio della continuità e derivabilità di una funzione al variare del parametro k YouTube

I teoremi delle funzioni derivabili ppt scaricare

Determinare se una funzione è continua YouTube

Continuità di una funzione Andrea il Matematico

La funzione Seno é Derivabile su R iMathematica

Continuità e derivabilità di una funzione.

Tutte le funzioni Derivabili sono Continue? YouTube

Ep.10 Derivata della funzione esponenziale Derivate YouTube

Derivata della funzione integrale TUTTI I CASI Esempi svolti YouTube

PPT LA DERIVATA DI UNA FUNZIONE PowerPoint Presentation, free download ID2434290

Se una funzione è derivabile non implica che la funzione è necessariamente continua. Se una funzione è differenziabile allora ammette tutte le derivate direzionali e inoltre è possibile calcolare le derivate direzionali senza usare il limite ma usando questa formula:. Teorema. Sia una funzione derivabile in . Allora è continua in . Dimostrazione. Vogliamo provare che. Per ipotesi. Possiamo scrivere. e, passando al limite per si ottiene. CVD. Non vale il viceversa! Come accade sempre in questi casi, per provare la falsità dell'implicazione inversa è sufficiente esibire un controesempio.